Das Webangebot www.xlog.ch kann mittels Textsuche durchsucht werden. Dazu wird im Suchfeld ein Suchausdruck eingegeben. Es erscheint darauf eine Trefferliste. Aus der Trefferliste kann ein Dokument ausgewählt werden. Das Ranking der Treffer ist im Folgenden genauer beschrieben.

Das Ranking beurteilt den Treffer auf der Seite, sowie den Beitrag jeder anderen Seite. Gibt es einen Treffer auf der Seite, so ist der Beitrag (1-λ)/τ, andernfalls ist der Beitrag λ/τ. Dies lässt sich grafisch folgendermassen Veranschaulichen:

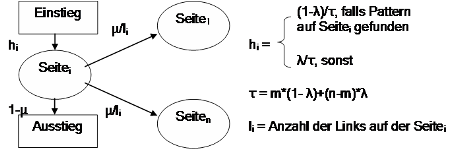
Dadurch dass das Ranking auch Seiten ohne Treffer einbezieht ist das Ranking eine Mischung aus einer allgemeinen Gewichtung der Seite innerhalb der ganzen Kollektion und einer Gewichtung in Bezug auf die Seiten innerhalb der Kollektion die das gegebene Pattern treffen. Da Links zwischen den Seiten jedoch in Zyklen münden können, ergibt sich für den Rank eine rekursive Matrixgleichung der folgenden Art: 

Wir lösen diese Gleichung exakt indem wir R = (E-L)^-1*H berechnen. Die Matrixinversion (E-L)^-1 wird für die Website nur einmal vor berechnet und über die Seiten hinweg gespeichert. Bei jeder Suche wird nur H erneut bestimmt und die Matrixmultiplikation durchgeführt. Dadurch gibt sich ein Verfahren das bei den Abfragen quadratisch in der Zeit ist, und nicht kubisch.